Paragon Tech - Markov Chains
This post describes the mathematical importance of Markov Chains, how they are used, and an amusing example using the script of Shrek.
You're probably familiar with generative AI models, like ChatGPT and others. Sometimes people will refer to generative AI as a "text predicting" algorithm. Recently, these models have become much more advanced, but it's still good to be aware of simple predictive models, like the Markov Chain.
Mathematical Background
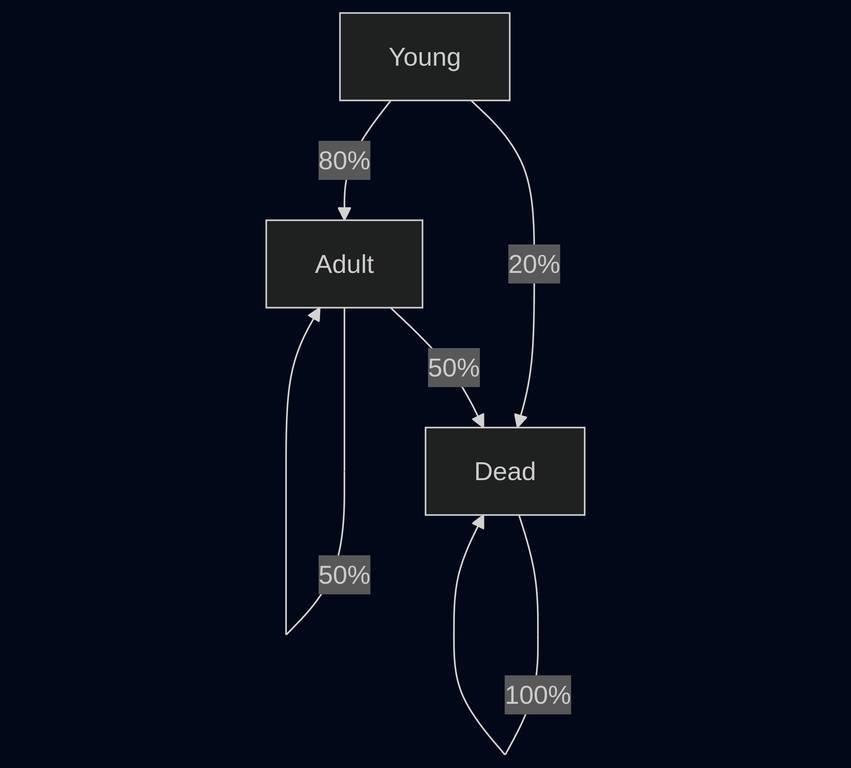
One simple predictive model is called the Markov Chain. A Markov Chain describes a process which is stochastic (variable by nature) where the next state can be predicted by the current state without considering the history of prior states. One example of this would be for population modeling. Consider a population of deer living in the wild. A deer can be in one of three states: [Young, Adult, Dead]. A young deer has a 80% chance of surviving to adulthood and a 20% chance of dying before reaching adulthood. An adult deer may have a 50% chance of surviving and a 50% of dying. Each of these changes can be modeled in a matrix, with each cell representing the probability of the next successive state. The matrix that describes this is called the Transition Matrix.
| Young | Adult | Dead | |
| Young | 0 | 0.8 | 0.2 |
| Adult | 0 | 0.5 | 0.5 |
| Dead | 0 | 0 | 1 |
The same scenario can be represented in graph form.
Another example would be modeling the state of a machine in a manufacturing environment. For example, a machine can be in states [Running, Idle, Down]. A running machine has a 90% chance of continuing to run and a 5% chance each for going idle or down. An idle machine has a 70% chance to run again, and 30% chance of staying idle. A down machine has a 20% chance to be repaired and sit idle, and a 80% chance to stay down.
| Running (R) | Idle (I) | Down (D) | |
| Running (R) | 0.9 | 0.05 | 0.05 |
| Idle (I) | 0.7 | 0.3 | 0 |
| Down (D) | 0 | 0.2 | 0.8 |
Notice that each row adds up to 1. Mathematically, we can predict the long-term state of a machine given this matrix.

We define a vector, pi, as the steady state vector, representing the probability of the machine in each of the three states. We know that this is a unit vector (all elements sum to 1) by definition. We also know that the probability of each state is the sum of the probabilities of transitioning into that state. This gives us a system of four equations with three unknowns, which can be solved.

By solving this system of equations, we can show that the steady-state probability of the machine is 70% running, 20% idle, and 10% down. This is a simple example, but it shows the basic mechanics of this predictive model. Markov Chains can be expanded into higher order models. Consider that this matrix is now a 3D matrix, with each layer of the matrix representing the prior state. Now the next state is dependent upon the current state and the prior state. This provides a more accurate model, and is still quick (for computers) to solve.
Fun with Text Prediction
Now let's have some fun with these models. If we take a sufficiently large sample of text, and use it to generate the transition matrix, we can emulate a generative text model. If we provide a starting word, the model should be able to predict the next word, then the next, and so on. For this example, I will write a small program in Rust and use the script of Shrek as the training data. Let's get into it!
First of all, we need to clean up the text file, set the entire thing to uppercase, and remove all punctuation. This ensures that "this" and "This" are treated equally. I use two functions to handle the text file clean up and splitting it into a vector of individual words.
fn open_file(path: &str) -> String {fs::read_to_string(path).unwrap().to_uppercase().replace(&['.', '!', '?', '\n', '\r', '-', '\'', '"', '{', '}', ','][..], "").split_whitespace().collect::<Vec<_>>().join(" ")}fn text_to_vec(input_text:&String)->Vec<String>{return input_text.split(" ").map(|s| s.to_string()).collect();}
Next up, we prompt the user for the starting word, the number of words to generate, and the file name for the training data. In my case, I used the entire script of the movie Shrek.
fn main() {let mut starting_word = String::new();let mut num_iterations_str = String::new();let mut input_file = String::new();print!("Enter starting word: ");io::stdout().flush().unwrap();io::stdin().read_line(&mut starting_word).unwrap();print!("Enter number of iterations: ");io::stdout().flush().unwrap();io::stdin().read_line(&mut num_iterations_str).unwrap();print!("Enter input file path: ");io::stdout().flush().unwrap();io::stdin().read_line(&mut input_file).unwrap();let starting_word = starting_word.trim().to_string().to_uppercase();let num_iterations: u16 = num_iterations_str.trim().parse().unwrap();let input_file = input_file.trim().to_string();
Next, we loop through all words in the training data, and for each unique word, we add it to a vector. We use a hash map to relate the vector of unique words with another vector for all of the words that follow it. If the same word follows multiple times, it will receive multiple entries in the second vector, increasing the likelihood that it's chosen as the next word.
// Vector of all strings in the training textlet text_elements = text_to_vec(&open_file(&input_file));// Hash map to hold the unique String keys and the list of their next wordslet mut hash_map : HashMap<String,Vec<String>> = HashMap::new();// Loop through all words to add to hash mapfor (index, element) in text_elements.iter().enumerate(){if index < text_elements.len() - 1{// If the hash map doesn't yet contain the current word as a keyif !hash_map.contains_key(element){// add the next word as new vectorhash_map.insert(String::from(element), vec![text_elements[index+1].to_string()]);}else{// Append the next word to the already exiting Vec<String> of next wordshash_map.get_mut(element).unwrap().push(text_elements[index+1].to_string());}}}
Now that we have the hash map of unique words and the vector of their following words, we start with the user's given starting word and begin randomly sampling.
let mut rng = rand::rng();// Make a vector for the sentence starting with the starting_wordlet mut sentence:Vec<String> = vec![starting_word];for item in 0..num_iterations-1{let current_word = sentence.get(usize::from(item)).unwrap();let rng_range = hash_map.get(current_word).unwrap().len();let random_index = rng.random_range(0..rng_range);let next_word = &hash_map.get(current_word).unwrap()[random_index];sentence.push(next_word.to_string());}println!("{:?}", sentence);
That's it! Here's an example of the output. You can tell that it almost makes sense, but of course the broader context and meaning is missing. This example is a first-order Markov Chain, so the next word is predicted using only the current word. A higher order Markov Chain may provide more coherent results.
["DONKEY", "RIGHT", "BEHIND", "YOU", "DO", "LIKE", "CAKES", "HAVE", "THE", "POINT", "WAIT", "YOU", "MUST", "EVER", "AFTER", "TIME", "HEY", "I", "LIKE", "ONIONS"]
Conclusion
I hope you found this description of Markov Chains educational. It's a useful tool for modeling state transitions when the prior states can be ignored. The long-term states are easily calculable and the model can simulated with a short program.
No comments yet. Login to start a new discussion Start a new discussion